数据结构JavaScript实例学习与研究
本文是对国内外大学教材和专业出版书籍的自主学习和总结,部分代码和文字说明均出自书籍(文章中某些原创的个人见解和内容没有一一标注,请自行甄别),也可能会有自己的理解和改动,以及平时的实战积累与逻辑转化。
既然是写程序,绝对少不了数据结构与算法,自己看过了三种不同的数据结构与算法书籍,虽然大同小异,但是总有一些查缺补漏,为了更好地作为温故而知新的学习材料,这里系统化的进行一次整理。本文列出了栈、队列、链表、字典、集合、散列表、二叉树、平衡二叉树、堆(二叉堆)、图的JavaScript的例子,结合书籍的理论,可以更好地去在实践中理解。
分类
参考计算机科学导论(英文原版和国内版大学教材,数据结构考研教材)
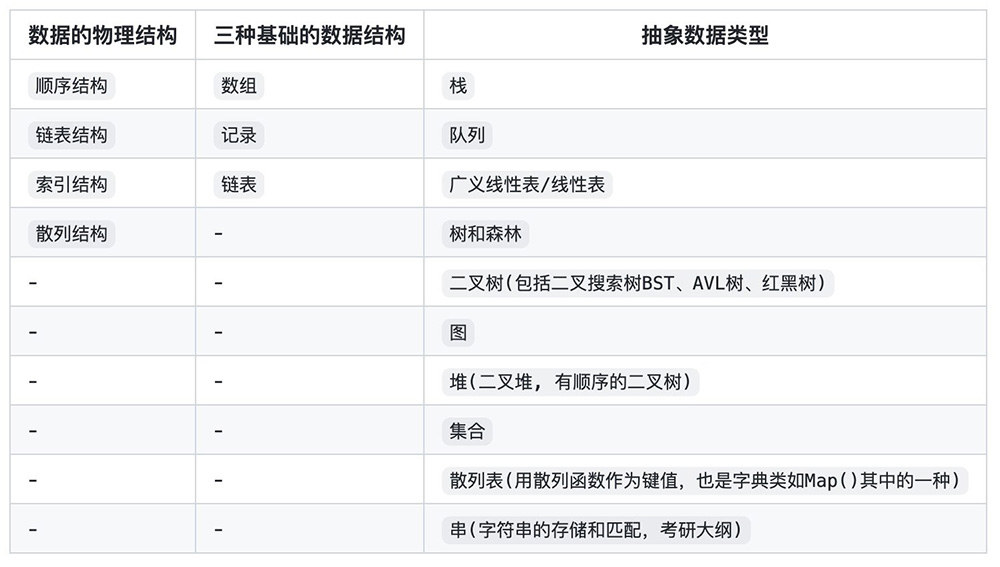
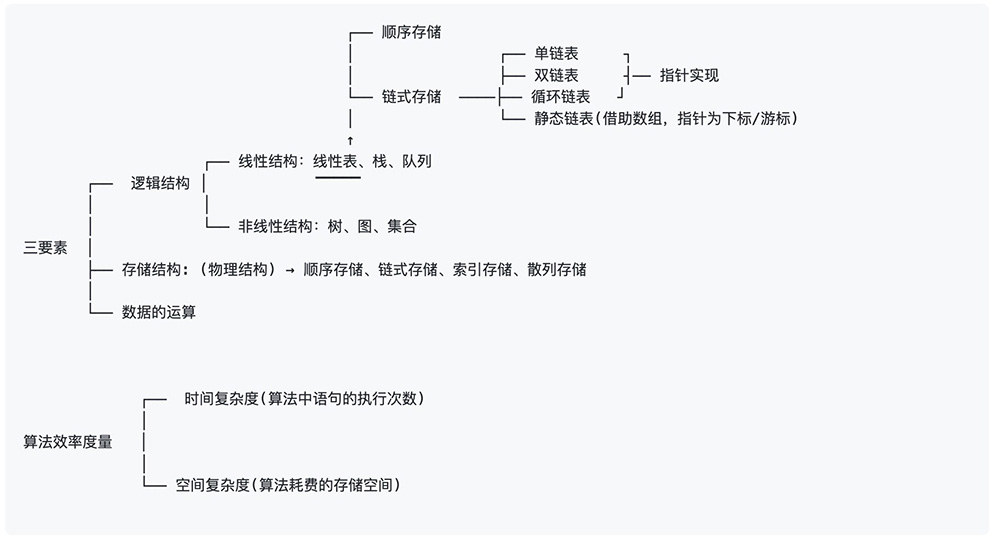
数据结构导图(考研指导)
栈(数组写法)
后进先出(LIFO),如堆放书本。
class StackArray {
constructor() {
this.items = [];
}
push(element) {
this.items.push(element);
}
pop() {
return this.items.pop();
}
peek() {
return this.items[this.items.length - 1];
}
isEmpty() {
return this.items.length === 0;
}
size() {
return this.items.length;
}
clear() {
this.items = [];
}
toArray() {
return this.items;
}
toString() {
return this.items.toString();
}
}
转化为ES5(Babel编译后):
"use strict";
function _classCallCheck(instance, Constructor) {
if (! (instance instanceof Constructor)) {
throw new TypeError("Cannot call a class as a function");
}
}
function _defineProperties(target, props) {
for (let i = 0; i < props.length; i++) {
const descriptor = props[i];
descriptor.enumerable = descriptor.enumerable || false;
descriptor.configurable = true;
if ("value" in descriptor) descriptor.writable = true;
Object.defineProperty(target, descriptor.key, descriptor);
}
}
function _createClass(Constructor, protoProps, staticProps) {
if (protoProps) _defineProperties(Constructor.prototype, protoProps);
if (staticProps) _defineProperties(Constructor, staticProps);
Object.defineProperty(Constructor, "prototype", {
writable: false
});
return Constructor;
}
const StackArray =
/*#__PURE__*/
function() {
function StackArray() {
_classCallCheck(this, StackArray);
this.items = [];
}
_createClass(StackArray, [{
key: "push",
value: function push(element) {
this.items.push(element);
}
},
{
key: "pop",
value: function pop() {
return this.items.pop();
}
},
...]);
return StackArray;
} ();
写成构造函数形式:
(第一种)
const StackArray = function () {
this.items = [];
}
StackArray.prototype.push = function (element) {
this.items.push(element);
}
const obj = new StackArray();
obj.push(1);
obj.push(2);
console.log(obj); // {items: [1,2])}
(第二种) - 闭包需要return一个对象,否则无法找到相应的方法
const StackArray = (function () {
'use strict';
//this.items = []; //如果这里写一个,就报错: Uncaught TypeError: Cannot set properties of undefined (setting 'items')
const myConstructor = function () {
this.items = [];
}
//添加属性
myConstructor.prototype.push = function (element) {
this.items.push(element);
}
return myConstructor;
})();
const obj = new StackArray();
obj.push(1);
obj.push(2);
console.log(obj); // {items: [1,2])}
(第三种)
const StackArray = (function () {
'use strict';
const myConstructor = function () {
this.items = [];
}
//实例化
const myInstance = function() {
return new myConstructor();
};
//添加属性
myConstructor.prototype.push = function (element) {
this.items.push(element);
return this; //返回对象后才能直接调用this.items的值, 没有return将返回错误:Uncaught TypeError: Cannot read properties of undefined (reading 'push')
}
return myInstance;
})();
console.log(StackArray().push(1).push(2)); // {items: [1,2])}
(第四种)不使用自执行
const StackArray = function () {
'use strict';
const myConstructor = function () {
this.items = [];
}
//实例化
const myInstance = function() {
return new myConstructor();
};
//添加属性
myConstructor.prototype.push = function (element) {
this.items.push(element);
return this; //返回对象后才能直接调用this.items的值, 没有return将返回错误:Uncaught TypeError: Cannot read properties of undefined (reading 'push')
}
return myInstance;
};
const fn = StackArray();
console.log(fn().push(1).push(2)); // {items: [1,2])}
栈(对象写法)
class Stack {
constructor() {
this.count = 0;
this.items = {};
}
push(element) {
this.items[this.count] = element;
this.count++;
}
pop() {
if (this.isEmpty()) {
return undefined;
}
this.count--;
const result = this.items[this.count];
delete this.items[this.count];
return result;
}
peek() {
if (this.isEmpty()) {
return undefined;
}
return this.items[this.count - 1];
}
isEmpty() {
return this.count === 0;
}
size() {
return this.count;
}
clear() {
/* while (!this.isEmpty()) {
this.pop();
} */
this.items = {};
this.count = 0;
}
toString() {
if (this.isEmpty()) {
return '';
}
let objString = `${this.items[0]}`;
for (let i = 1; i < this.count; i++) {
objString = `${objString},${this.items[i]}`;
}
return objString;
}
}
队列
先进先出(FIFO),如排队,等电话
class Queue {
constructor() {
this.count = 0;
this.lowestCount = 0;
this.items = {};
}
enqueue(element) {
this.items[this.count] = element;
this.count++;
}
dequeue() {
if (this.isEmpty()) {
return undefined;
}
const result = this.items[this.lowestCount];
delete this.items[this.lowestCount];
this.lowestCount++;
return result;
}
peek() {
if (this.isEmpty()) {
return undefined;
}
return this.items[this.lowestCount];
}
isEmpty() {
return this.size() === 0;
}
clear() {
this.items = {};
this.count = 0;
this.lowestCount = 0;
}
size() {
return this.count - this.lowestCount;
}
toString() {
if (this.isEmpty()) {
return '';
}
let objString = `${this.items[this.lowestCount]}`;
for (let i = this.lowestCount + 1; i < this.count; i++) {
objString = `${objString},${this.items[i]}`;
}
return objString;
}
}
//使用
const q = new Queue();
q.enqueue(1);
q.enqueue(2);
q.enqueue(3);
console.log(q);
/*
{
"count": 3,
"lowestCount": 0,
"items": {
"0": 1,
"1": 2,
"2": 3
}
}
*/
const q2 = new Queue();
q2.enqueue(1);
q2.enqueue(2);
q2.enqueue(3);
q2.dequeue();
console.log(q2);
/*
{
"count": 3,
"lowestCount": 1,
"items": {
"1": 2,
"2": 3
}
}
注意:如果不声明q2 = new Queue(),直接使用q,则两个console.log中的items都只输出显示2个元素,count和lowestCount都是一样的显示。
*/
双端队列
class Deque {
constructor() {
this.count = 0;
this.lowestCount = 0;
this.items = {};
}
addFront(element) {
if (this.isEmpty()) {
this.addBack(element);
} else if (this.lowestCount > 0) {
this.lowestCount--;
this.items[this.lowestCount] = element;
} else {
for (let i = this.count; i > 0; i--) {
this.items[i] = this.items[i - 1];
}
this.count++;
this.items[0] = element;
}
}
addBack(element) {
this.items[this.count] = element;
this.count++;
}
removeFront() {
if (this.isEmpty()) {
return undefined;
}
const result = this.items[this.lowestCount];
delete this.items[this.lowestCount];
this.lowestCount++;
return result;
}
removeBack() {
if (this.isEmpty()) {
return undefined;
}
this.count--;
const result = this.items[this.count];
delete this.items[this.count];
return result;
}
peekFront() {
if (this.isEmpty()) {
return undefined;
}
return this.items[this.lowestCount];
}
peekBack() {
if (this.isEmpty()) {
return undefined;
}
return this.items[this.count - 1];
}
isEmpty() {
return this.size() === 0;
}
clear() {
this.items = {};
this.count = 0;
this.lowestCount = 0;
}
size() {
return this.count - this.lowestCount;
}
toString() {
if (this.isEmpty()) {
return '';
}
let objString = `${this.items[this.lowestCount]}`;
for (let i = this.lowestCount + 1; i < this.count; i++) {
objString = `${objString},${this.items[i]}`;
}
return objString;
}
}
//使用(注意addFront方法导致3排在最前,addBack方法导致3排在了最后)
const q = new Deque();
q.addFront(1);
q.addFront(2);
q.addFront(3);
console.log(q);
/*
{
"count": 3,
"lowestCount": 0,
"items": {
"0": 3,
"1": 2,
"2": 1
}
}
*/
const q2 = new Deque();
q2.addBack(1);
q2.addBack(2);
q2.addBack(3);
console.log(q2);
/*
{
"count": 3,
"lowestCount": 0,
"items": {
"0": 1,
"1": 2,
"2": 3
}
}
*/
单向链表
//比较节点
function defaultEquals(a, b) {
return a === b;
}
//助手类
class Node {
constructor(element, next) {
this.element = element;
this.next = next;
}
}
//-------
class LinkedList {
constructor(equalsFn = defaultEquals) {
this.equalsFn = equalsFn;
this.count = 0;
this.head = undefined;
}
push(element) {
const node = new Node(element);
let current;
if (this.head == null) {
// catches null && undefined
this.head = node;
} else {
current = this.head;
while (current.next != null) {
current = current.next;
}
current.next = node;
}
this.count++;
}
getElementAt(index) {
if (index >= 0 && index <= this.count) {
let node = this.head;
for (let i = 0; i < index && node != null; i++) {
node = node.next;
}
return node;
}
return undefined;
}
insert(element, index) {
if (index >= 0 && index <= this.count) {
const node = new Node(element);
if (index === 0) {
const current = this.head;
node.next = current;
this.head = node;
} else {
const previous = this.getElementAt(index - 1);
node.next = previous.next;
previous.next = node;
}
this.count++;
return true;
}
return false;
}
removeAt(index) {
if (index >= 0 && index < this.count) {
let current = this.head;
if (index === 0) {
this.head = current.next;
} else {
const previous = this.getElementAt(index - 1);
current = previous.next;
previous.next = current.next;
}
this.count--;
return current.element;
}
return undefined;
}
remove(element) {
const index = this.indexOf(element);
return this.removeAt(index);
}
indexOf(element) {
let current = this.head;
for (let i = 0; i < this.size() && current != null; i++) {
if (this.equalsFn(element, current.element)) {
return i;
}
current = current.next;
}
return -1;
}
isEmpty() {
return this.size() === 0;
}
size() {
return this.count;
}
getHead() {
return this.head;
}
clear() {
this.head = undefined;
this.count = 0;
}
toString() {
if (this.head == null) {
return '';
}
let objString = `${this.head.element}`;
let current = this.head.next;
for (let i = 1; i < this.size() && current != null; i++) {
objString = `${objString},${current.element}`;
current = current.next;
}
return objString;
}
}
双向链表(继承单向链表的类)
//比较节点
function defaultEquals(a, b) {
return a === b;
}
//助手类
class Node {
constructor(element, next) {
this.element = element;
this.next = next;
}
}
class DoublyNode extends Node {
constructor(element, next, prev) {
super(element, next); //调用Node()的构造函数(和constructor()的参数相对应,可以比constructor()的参数少)
this.prev = prev; //新增
}
}
//--------
class DoublyLinkedList extends LinkedList {
constructor(equalsFn = defaultEquals) {
super(equalsFn); //调用LinkedList()的构造函数
this.tail = undefined; //新增
}
push(element) {
const node = new DoublyNode(element);
if (this.head == null) {
this.head = node;
this.tail = node; // NEW
} else {
// attach to the tail node // NEW
this.tail.next = node;
node.prev = this.tail;
this.tail = node;
}
this.count++;
}
insert(element, index) {
if (index >= 0 && index <= this.count) {
const node = new DoublyNode(element);
let current = this.head;
if (index === 0) {
if (this.head == null) { // NEW
this.head = node;
this.tail = node; // NEW
} else {
node.next = this.head;
this.head.prev = node; // NEW
this.head = node;
}
} else if (index === this.count) { // last item NEW
current = this.tail;
current.next = node;
node.prev = current;
this.tail = node;
} else {
const previous = this.getElementAt(index - 1);
current = previous.next;
node.next = current;
previous.next = node;
current.prev = node; // NEW
node.prev = previous; // NEW
}
this.count++;
return true;
}
return false;
}
removeAt(index) {
if (index >= 0 && index < this.count) {
let current = this.head;
if (index === 0) {
this.head = this.head.next;
// if there is only one item, then we update tail as well //NEW
if (this.count === 1) {
// {2}
this.tail = undefined;
} else {
this.head.prev = undefined;
}
} else if (index === this.count - 1) {
// last item //NEW
current = this.tail;
this.tail = current.prev;
this.tail.next = undefined;
} else {
current = this.getElementAt(index);
const previous = current.prev;
// link previous with current's next - skip it to remove
previous.next = current.next;
current.next.prev = previous; // NEW
}
this.count--;
return current.element;
}
return undefined;
}
indexOf(element) {
let current = this.head;
let index = 0;
while (current != null) {
if (this.equalsFn(element, current.element)) {
return index;
}
index++;
current = current.next;
}
return -1;
}
getHead() {
return this.head;
}
getTail() {
return this.tail;
}
clear() {
super.clear();
this.tail = undefined;
}
toString() {
if (this.head == null) {
return '';
}
let objString = `${this.head.element}`;
let current = this.head.next;
while (current != null) {
objString = `${objString},${current.element}`;
current = current.next;
}
return objString;
}
inverseToString() {
if (this.tail == null) {
return '';
}
let objString = `${this.tail.element}`;
let previous = this.tail.prev;
while (previous != null) {
objString = `${objString},${previous.element}`;
previous = previous.prev;
}
return objString;
}
}
双向链表+栈的数据结构混合
import DoublyLinkedList from './doubly-linked-list';
export default class StackLinkedList {
constructor() {
this.items = new DoublyLinkedList();
}
push(element) {
this.items.push(element);
}
pop() {
if (this.isEmpty()) {
return undefined;
}
const result = this.items.removeAt(this.size() - 1);
return result;
}
peek() {
if (this.isEmpty()) {
return undefined;
}
return this.items.getElementAt(this.size() - 1).element;
}
isEmpty() {
return this.items.isEmpty();
}
size() {
return this.items.size();
}
clear() {
this.items.clear();
}
toString() {
return this.items.toString();
}
}
有序链表
import { Compare, defaultCompare, defaultEquals } from '../util';
import LinkedList from './linked-list';
export default class SortedLinkedList extends LinkedList {
constructor(equalsFn = defaultEquals, compareFn = defaultCompare) {
super(equalsFn);
this.equalsFn = equalsFn;
this.compareFn = compareFn;
}
push(element) {
if (this.isEmpty()) {
super.push(element);
} else {
const index = this.getIndexNextSortedElement(element);
super.insert(element, index);
}
}
insert(element, index = 0) {
if (this.isEmpty()) {
return super.insert(element, index === 0 ? index : 0);
}
const pos = this.getIndexNextSortedElement(element);
return super.insert(element, pos);
}
getIndexNextSortedElement(element) {
let current = this.head;
let i = 0;
for (; i < this.size() && current; i++) {
const comp = this.compareFn(element, current.element);
if (comp === Compare.LESS_THAN) {
return i;
}
current = current.next;
}
return i;
}
}
循环链表
import { defaultEquals } from '../util';
import LinkedList from './linked-list';
import { Node } from './models/linked-list-models';
export default class CircularLinkedList extends LinkedList {
constructor(equalsFn = defaultEquals) {
super(equalsFn);
}
push(element) {
const node = new Node(element);
let current;
if (this.head == null) {
this.head = node;
} else {
current = this.getElementAt(this.size() - 1);
current.next = node;
}
// set node.next to head - to have circular list
node.next = this.head;
this.count++;
}
insert(element, index) {
if (index >= 0 && index <= this.count) {
const node = new Node(element);
let current = this.head;
if (index === 0) {
if (this.head == null) {
// if no node in list
this.head = node;
node.next = this.head;
} else {
node.next = current;
current = this.getElementAt(this.size());
// update last element
this.head = node;
current.next = this.head;
}
} else {
const previous = this.getElementAt(index - 1);
node.next = previous.next;
previous.next = node;
}
this.count++;
return true;
}
return false;
}
removeAt(index) {
if (index >= 0 && index < this.count) {
let current = this.head;
if (index === 0) {
if (this.size() === 1) {
this.head = undefined;
} else {
const removed = this.head;
current = this.getElementAt(this.size() - 1);
this.head = this.head.next;
current.next = this.head;
current = removed;
}
} else {
// no need to update last element for circular list
const previous = this.getElementAt(index - 1);
current = previous.next;
previous.next = current.next;
}
this.count--;
return current.element;
}
return undefined;
}
}
字典(类似原生Map()类)
function defaultToString(item) {
if (item === null) {
return 'NULL';
} if (item === undefined) {
return 'UNDEFINED';
} if (typeof item === 'string' || item instanceof String) {
return `${item}`;
}
return item.toString();
}
class ValuePair {
constructor(key, value) {
this.key = key;
this.value = value;
}
toString() {
return `[#${this.key}: ${this.value}]`;
}
}
//---------
class Dictionary {
constructor(toStrFn = defaultToString) {
this.toStrFn = toStrFn;
this.table = {};
}
set(key, value) {
if (key != null && value != null) {
const tableKey = this.toStrFn(key);
this.table[tableKey] = new ValuePair(key, value);
return true;
}
return false;
}
get(key) {
const valuePair = this.table[this.toStrFn(key)];
return valuePair == null ? undefined : valuePair.value;
}
hasKey(key) {
return this.table[this.toStrFn(key)] != null;
}
remove(key) {
if (this.hasKey(key)) {
delete this.table[this.toStrFn(key)];
return true;
}
return false;
}
values() {
return this.keyValues().map(valuePair => valuePair.value);
}
keys() {
return this.keyValues().map(valuePair => valuePair.key);
}
keyValues() {
return Object.values(this.table);
}
forEach(callbackFn) {
const valuePairs = this.keyValues();
for (let i = 0; i < valuePairs.length; i++) {
const result = callbackFn(valuePairs[i].key, valuePairs[i].value);
if (result === false) {
break;
}
}
}
isEmpty() {
return this.size() === 0;
}
size() {
return Object.keys(this.table).length;
}
clear() {
this.table = {};
}
toString() {
if (this.isEmpty()) {
return '';
}
const valuePairs = this.keyValues();
let objString = `${valuePairs[0].toString()}`;
for (let i = 1; i < valuePairs.length; i++) {
objString = `${objString},${valuePairs[i].toString()}`;
}
return objString;
}
}
散列表
(其实就是将字典类的 key值使用散列函数换成 "纯数字" 作为键值)
function defaultToString(item) {
if (item === null) {
return 'NULL';
} if (item === undefined) {
return 'UNDEFINED';
} if (typeof item === 'string' || item instanceof String) {
return `${item}`;
}
return item.toString();
}
class ValuePair {
constructor(key, value) {
this.key = key;
this.value = value;
}
toString() {
return `[#${this.key}: ${this.value}]`;
}
}
//---------
class HashTable {
constructor(toStrFn = defaultToString) {
this.toStrFn = toStrFn;
this.table = {};
}
loseloseHashCode(key) {
if (typeof key === 'number') {
return key;
}
const tableKey = this.toStrFn(key);
let hash = 0;
for (let i = 0; i < tableKey.length; i++) {
hash += tableKey.charCodeAt(i);
}
return hash % 37;
}
/* djb2HashCode(key) {
const tableKey = this.toStrFn(key);
let hash = 5381;
for (let i = 0; i < tableKey.length; i++) {
hash = (hash * 33) + tableKey.charCodeAt(i);
}
return hash % 1013;
} */
hashCode(key) {
return this.loseloseHashCode(key);
}
put(key, value) {
if (key != null && value != null) {
const position = this.hashCode(key);
this.table[position] = new ValuePair(key, value);
return true;
}
return false;
}
get(key) {
const valuePair = this.table[this.hashCode(key)];
return valuePair == null ? undefined : valuePair.value;
}
remove(key) {
const hash = this.hashCode(key);
const valuePair = this.table[hash];
if (valuePair != null) {
delete this.table[hash];
return true;
}
return false;
}
getTable() {
return this.table;
}
isEmpty() {
return this.size() === 0;
}
size() {
return Object.keys(this.table).length;
}
clear() {
this.table = {};
}
toString() {
if (this.isEmpty()) {
return '';
}
const keys = Object.keys(this.table);
let objString = `{${keys[0]} => ${this.table[keys[0]].toString()}}`;
for (let i = 1; i < keys.length; i++) {
objString = `${objString},{${keys[i]} => ${this.table[keys[i]].toString()}}`;
}
return objString;
}
}
集合(实现原生Set()类)
class Set {
constructor() {
this.items = {};
}
add(element) {
if (!this.has(element)) {
this.items[element] = element;
return true;
}
return false;
}
delete(element) {
if (this.has(element)) {
delete this.items[element];
return true;
}
return false;
}
has(element) {
return Object.prototype.hasOwnProperty.call(this.items, element);
}
values() {
return Object.values(this.items);
}
union(otherSet) {
const unionSet = new Set();
this.values().forEach(value => unionSet.add(value));
otherSet.values().forEach(value => unionSet.add(value));
return unionSet;
}
intersection(otherSet) {
const intersectionSet = new Set();
const values = this.values();
const otherValues = otherSet.values();
let biggerSet = values;
let smallerSet = otherValues;
if (otherValues.length - values.length > 0) {
biggerSet = otherValues;
smallerSet = values;
}
smallerSet.forEach(value => {
if (biggerSet.includes(value)) {
intersectionSet.add(value);
}
});
return intersectionSet;
}
difference(otherSet) {
const differenceSet = new Set();
this.values().forEach(value => {
if (!otherSet.has(value)) {
differenceSet.add(value);
}
});
return differenceSet;
}
isSubsetOf(otherSet) {
if (this.size() > otherSet.size()) {
return false;
}
let isSubset = true;
this.values().every(value => {
if (!otherSet.has(value)) {
isSubset = false;
return false;
}
return true;
});
return isSubset;
}
isEmpty() {
return this.size() === 0;
}
size() {
return Object.keys(this.items).length;
}
clear() {
this.items = {};
}
toString() {
if (this.isEmpty()) {
return '';
}
const values = this.values();
let objString = `${values[0]}`;
for (let i = 1; i < values.length; i++) {
objString = `${objString},${values[i].toString()}`;
}
return objString;
}
}
构造二叉搜索树(左侧节点小于父节点,右侧节点大于父节点)
【构造二叉搜索树(左侧节点小于父节点,右侧节点大于父节点)需要使用递归,遍历树也需要使用递归】
遍历方式:
- 1.广度优先(breadth-first searh, BFS)
先处理子节点,再进行下一层
- 2.深度优先(depth-first search,DFS)
前序(先序),中序,后序
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1
};
function defaultCompare(a, b) {
if (a === b) {
return 0;
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
//助手类
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
toString() {
return `${this.key}`;
}
}
class BinarySearchTree {
constructor(compareFn = defaultCompare) {
this.compareFn = compareFn;
this.root = null;
}
getRoot() {
return this.root;
}
//插入节点
//---------
insert(key) {
// special case: first key
if (this.root == null) {
this.root = new Node(key);
} else {
this.insertNode(this.root, key);
}
}
insertNode(node, key) {
if (this.compareFn(key, node.key) === Compare.LESS_THAN) { //新节点的键小于当前节点的键
if (node.left == null) {
node.left = new Node(key);
} else {
this.insertNode(node.left, key);
}
} else if (node.right == null) {
node.right = new Node(key);
} else {
this.insertNode(node.right, key);
}
}
//搜索节点
//---------
search(key) {
return this.searchNode(this.root, key);
}
searchNode(node, key) {
if (node == null) {
return false;
}
if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
return this.searchNode(node.left, key);
} if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
return this.searchNode(node.right, key);
}
return true;
}
//中序遍历
//---------
inOrderTraverse(callback) {
this.inOrderTraverseNode(this.root, callback);
}
inOrderTraverseNode(node, callback) {
if (node != null) {
this.inOrderTraverseNode(node.left, callback);
callback(node.key);
this.inOrderTraverseNode(node.right, callback);
}
}
//前序(先序)遍历
//---------
preOrderTraverse(callback) {
this.preOrderTraverseNode(this.root, callback);
}
preOrderTraverseNode(node, callback) {
if (node != null) {
callback(node.key); //先访问父节点
this.preOrderTraverseNode(node.left, callback);
this.preOrderTraverseNode(node.right, callback);
}
}
//后续遍历
//---------
postOrderTraverse(callback) {
this.postOrderTraverseNode(this.root, callback);
}
postOrderTraverseNode(node, callback) {
if (node != null) {
this.postOrderTraverseNode(node.left, callback);
this.postOrderTraverseNode(node.right, callback);
callback(node.key); //最后访问父节点本身
}
}
//获取最小值
//---------
min() {
return this.minNode(this.root);
}
minNode(node) {
let current = node;
while (current != null && current.left != null) { //找最小值只需要搜索树的左边
current = current.left;
}
return current;
}
//获取最大值
//---------
max() {
return this.maxNode(this.root);
}
maxNode(node) {
let current = node;
while (current != null && current.right != null) { //找最大值只需要搜索树的→边
current = current.right;
}
return current;
}
//移除一个节点
//---------
remove(key) {
this.root = this.removeNode(this.root, key);
}
removeNode(node, key) {
if (node == null) { //基线条件
return null;
}
if (this.compareFn(key, node.key) === Compare.LESS_THAN) { //找的键比当前键小,则在左侧搜索
node.left = this.removeNode(node.left, key);
return node;
} if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
node.right = this.removeNode(node.right, key);
return node;
}
// key is equal to node.item
// handle 3 special conditions
// 1 - a leaf node
// 2 - a node with only 1 child
// 3 - a node with 2 children
// case 1 (第一种情况,键等于node.key,无子节点)
if (node.left == null && node.right == null) {
node = null;
return node;;
}
// case 2 (第二种情况,有一个左侧或者右侧子节点)
if (node.left == null) {
node = node.right;
return node;
} if (node.right == null) {
node = node.left;
return node;
}
// case 3 (第三种情况,有两个子节点的节点)
const aux = this.minNode(node.right); //当找到了要移除的节点后,需要找到它右边树中最小的节点
node.key = aux.key; //用最小的节点值更新这个节点值
node.right = this.removeNode(node.right, aux.key);
return node;
}
}
//用法
const tree = new BinarySearchTree();
tree.insert(11);
tree.insert(15);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.insert(20);
tree.insert(18);
tree.insert(25);
console.log(tree.root);
//结构输出如下:
/*
{
"key": 11,
"left": {
"key": 5,
"left": {
"key": 3,
"left": null,
"right": null
},
"right": {
"key": 9,
"left": {
"key": 8,
"left": null,
"right": null
},
"right": {
"key": 10,
"left": null,
"right": null
}
}
},
"right": {
"key": 15,
"left": {
"key": 13,
"left": {
"key": 12,
"left": null,
"right": null
},
"right": {
"key": 14,
"left": null,
"right": null
}
},
"right": {
"key": 20,
"left": {
"key": 18,
"left": null,
"right": null
},
"right": {
"key": 25,
"left": null,
"right": null
}
}
}
}
11
/ \
7 15
/ \ / \
5 9 13 20
/ / \ / \ / \
3 8 10 12 14 18 25
3为最小值,25为最大值
*/
中序遍历(上行顺序访问所有节点,即数值从小到大):
tree.inOrderTraverse( function(v) {
console.log(v);
// 3
// 5
// 8
// 9
// 10
// 11
// 12
// 13
// 14
// 15
// 18
// 20
// 25
});
前序(先序)遍历(优先于后代节点的顺序访问每个节点):
tree.preOrderTraverse( function(v) {
console.log(v);
// 11
// 5
// 3
// 9
// 8
// 10
// 15
// 13
// 12
// 14
// 20
// 18
// 25
});
后序遍历(先访问节点的后代节点,再访问节点本身):
tree.postOrderTraverse( function(v) {
console.log(v);
// 3
// 8
// 10
// 9
// 5
// 12
// 14
// 13
// 18
// 25
// 20
// 15
// 11
});
添加一个新节点6
tree.insert(6);
/*
11
/ \
7 15
/ \ / \
5 9 13 20
/ \ / \ / \ / \
3 6 8 10 12 14 18 25
*/
删除节点6(无子节点)
tree.remove(6);
/*
11
/ \
7 15
/ \ / \
5 9 13 20
/ / \ / \ / \
3 8 10 12 14 18 25
*/
删除节点5(有一个左边或右边子节点)
tree.remove(5);
/*
11
/ \
7 15
/ \ / \
3 9 13 20
/ \ / \ / \
8 10 12 14 18 25
*/
删除节点15(有两个子节点)
tree.remove(15);
/*
11
/ \
7 18 (删除的15被替换成18,保持BST结构)
/ \ / \
3 9 13 20
/ \ / \ \
8 10 12 14 25
*/
AVL(Adelson-Velskii-Landi)自平衡树(基于二叉搜索树)
如下面的BST,右侧节点非常长,需要平衡
/*
11
/ \
7 15
/ \ / \
5 9 13 20
/ \ / \ / \ / \
3 6 8 10 12 14 18 25
\
27
\
30
\
46
*/
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1
};
function defaultCompare(a, b) {
if (a === b) {
return 0;
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
//助手类
class Node {
constructor(key) {
this.key = key;
this.left = null;
this.right = null;
}
toString() {
return `${this.key}`;
}
}
//作为计数器的常量
const BalanceFactor = {
UNBALANCED_RIGHT: 1,
SLIGHTLY_UNBALANCED_RIGHT: 2,
BALANCED: 3,
SLIGHTLY_UNBALANCED_LEFT: 4,
UNBALANCED_LEFT: 5
};
class AVLTree extends BinarySearchTree {
constructor(compareFn = defaultCompare) {
super(compareFn);
this.compareFn = compareFn;
this.root = null;
}
getNodeHeight(node) {
if (node == null) {
return -1;
}
return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
}
/**
* Left left case: rotate right
* @param node Node
*/
//平衡操作:左-左(LL) => 向右的单旋转
//左侧子节点高度大于右侧子节点高度
/*
3
/
2
/
1
转变为:
2
/ \
1 3
实例(括号内的是高度差,节点30为平衡操作节点):
50(+2)~Y
(L)/ \
30(1) 70(0)
(L)/ \
10(1)~Z 40(0)~X
/
5(0)
转变为:
30(0)
/ \
10(1) 50(0)
/ / \
5(0) 40(0) 70(0)
*/
rotationLL(node) {
const tmp = node.left; //与平衡操作相关的节点有3个(~X,~Y,~Z), 将节点~X置于节点~Y(平衡因子为+2)所在的位置
node.left = tmp.right; // 将节点~Y的左子节点设置为节点~X的右子节点
tmp.right = node; //将节点~X的右子节点设置为节点~Y
return tmp;
}
/**
* Right right case: rotate left
* @param node Node
*/
//平衡操作:右-右(RR) => 向左的单旋转
//右侧子节点高度大于左侧子节点高度
/*
1
\
2
\
3
转变为:
2
/ \
1 3
实例(括号内的是高度差,节点70为平衡操作节点):
50(-2)
/ \
30(0) 70(-1)
/ \
60(0) 80(-1)
\
90(0)
转变为:
70(0)
/ \
50(0) 80(-1)
/ \ \
30(0) 60(0) 90(0)
*/
rotationRR(node) {
const tmp = node.right;
node.right = tmp.left;
tmp.left = node;
return tmp;
}
/**
* Left right case: rotate left then right
* @param node Node
*/
//平衡操作:左-右(LR) => 向右的双旋转 (先左旋转修复成LL, 再右旋转修复)
//左侧子节点高度大于右侧子节点高度,并且左侧子节点右侧较重
/*
3
/
1
\
2
左旋转:
3
/
2
/
1
右旋转:
2
/ \
1 3
实例(括号内的是高度差,节点30为平衡操作节点):
50(+2)
/ \
30(-1) 70(0)
/ \
10(0) 40(1)
/
35(0)
转变为:
40(0)
/ \
30(0) 50(-1)
/ \ \
10(0) 35(0) 70(0)
*/
rotationLR(node) {
node.left = this.rotationRR(node.left);
return this.rotationLL(node);
}
/**
* Right left case: rotate right then left
* @param node Node
*/
//平衡操作:右-左(RL) => 向左的双旋转 (先左旋转修复成LL, 再右旋转修复)
//右侧子节点高度大于左侧子节点高度,并且右侧子节点左侧较重
/*
1
\
3
/
2
右旋转:
1
\
2
\
3
左旋转:
2
/ \
1 3
实例(括号内的是高度差,节点80为平衡操作节点):
70(-2)
/ \
50(0) 80(1)
/ \
72(-1) 90(0)
\
75(0)
转变为:
72(-1)
/ \
70(-1) 80(0)
/ / \
50(0) 75(0) 90(0)
*/
rotationRL(node) {
node.right = this.rotationLL(node.right);
return this.rotationRR(node);
}
getBalanceFactor(node) {
const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
switch (heightDifference) {
case -2:
return BalanceFactor.UNBALANCED_RIGHT;
case -1:
return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;
case 1:
return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;
case 2:
return BalanceFactor.UNBALANCED_LEFT;
default:
return BalanceFactor.BALANCED;
}
}
insert(key) {
this.root = this.insertNode(this.root, key);
}
insertNode(node, key) {
if (node == null) {
return new Node(key);
} if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
node.left = this.insertNode(node.left, key);
} else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
node.right = this.insertNode(node.right, key);
} else {
return node; // 重复的键
}
// 如果需要,将树进行平衡操作
const balanceFactor = this.getBalanceFactor(node);
if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
if (this.compareFn(key, node.left.key) === Compare.LESS_THAN) {
// Left left case
node = this.rotationLL(node);
} else {
// Left right case
return this.rotationLR(node);
}
}
if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
if (this.compareFn(key, node.right.key) === Compare.BIGGER_THAN) {
// Right right case
node = this.rotationRR(node);
} else {
// Right left case
return this.rotationRL(node);
}
}
return node;
}
removeNode(node, key) {
node = super.removeNode(node, key); // 也可以使用BST的方法删除节点
if (node == null) {
return node; //null, 不需要进行平衡
}
// 检测树是否平衡
const balanceFactor = this.getBalanceFactor(node);
if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
// Left left case
if (
this.getBalanceFactor(node.left) === BalanceFactor.BALANCED
|| this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT
) {
return this.rotationLL(node);
}
// Left right case
if (this.getBalanceFactor(node.left) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {
return this.rotationLR(node.left);
}
}
if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
// Right right case
if (
this.getBalanceFactor(node.right) === BalanceFactor.BALANCED
|| this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT
) {
return this.rotationRR(node);
}
// Right left case
if (this.getBalanceFactor(node.right) === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {
return this.rotationRL(node.right);
}
}
return node;
}
}
红黑树(也是自平衡二叉搜索树)
如果插入和删除频率低,使用AVL比红黑树更好,否则使用红黑树更好
给插入的节点增加color和parent(双亲/父节点)属性以此来深入构造(注意父节点parent、祖父节点parent.parent, 叔节点parent.parent.right的填色和旋转)。
- 属性 #1: 红 - 黑树必须是二叉搜索树。
- 属性 #2: 根节点必须为黑色。
- 属性 #3: 红色节点的子节点必须是黑色的。 (不应有两个连续的 RED 节点)。
- 属性 #4: 在树的所有路径中,应该有相同数量的黑色节点。
- 属性 #5: 每个新节点都必须以红色插入。
- 属性 #6: 每个叶节点(即 NULL引用表示的 节点)必须涂成黑色。
其它概念(研究生方向)
- 树的存储结构: 顺序和链式
- 表示法: 双亲表示法,孩子表示法,孩子兄弟表示法
- 二叉链
- 森林(多个树构成森林)
- 哈夫曼编码
- 哈夫曼树
- 并查集
/*
一棵红黑树 —— []内代表红色:
6
/ \
2 [15]
/ \
11 18
/ \ \
[8] [14] [20]
将5,4,3,2,1依次插入红黑树的形态变化:
5 => 5 => 4 => 4 => 4
/ / \ / \ / \
[4] [3] [5] 3 5 2 5
/ / \
[2] [1] [3]
*/
const CONSTANTS = {
RED: 'RED',
BLACK: 'BLACK',
};
class Node {
constructor(param) {
this.key = param.key || 0;
this.color = param.color || CONSTANTS.RED;
this.left = param.left || undefined;
this.right = param.right || undefined;
this.parent = param.parent || undefined;
}
}
class RedBlackTree {
constructor() {
this.leaf = new Node({ key: 0, color: CONSTANTS.BLACK });
this.root = this.leaf;
}
//插入
//-----------------------------
insert({ key }) {
const node = new Node({
key,
left: this.leaf,
right: this.leaf,
});
let parent;
//将根节点设置为临时引用
let tmp = this.root;
// 寻找新节点的父节点
// 检查所有节点,但没有得到一个空叶子
while (tmp !== this.leaf) {
parent = tmp;
// 目标节点小于当前当前节点,则应该搜索左子树
if (node.key < tmp.key) {
tmp = tmp.left;
} else { // 目标节点大于当前当前节点,则应该搜索右子树
tmp = tmp.right;
}
}
node.parent = parent;
// 在左子树或右子树中插入节点
if (! parent) {
this.root = node;
} else if (node.key < parent.key) {
parent.left = node;
} else {
parent.right = node;
}
// 父节点不存在,则该节点将是根节点,并填色为”黑“
if (! node.parent) {
node.color = CONSTANTS.BLACK;
return;
}
// 节点没有祖父节点,所以我们没有平衡树
if (! node.parent.parent) {
return;
}
this.balanceInsert(node);
}
//平衡插入的节点
//-----------------------------
/*
插入后平衡树的方法:
1)在节点的父节点为"红色"时进行树的平衡。
2)如果节点的父节点是其祖父节点的左侧子节点:
a) 如果叔节点和父节点都是”红色“,我们可以将父节点和叔节点的颜色改为”黑色“,使祖父节点为”红色“,并为祖父节点应用平衡解决规则:红色节点的两个子节点都是黑色的。
b) 如果父节点是”红色“,叔节点是”黑色“。如果节点是右子节点,则对父节点应用平衡并向左旋转。将父代变为黑色,将祖代变为红色。为祖父节点应用向右旋转。
3)如果节点的父节点是右侧子节点:
a) 如果父节点和叔节点是”红色“,我们应该把他们变成”黑色“,把祖父节点变成”红色“。之后将对祖父节点应用平衡。
b) 否则,如果节点是左子节点,我们继续从父节点平衡并进行左旋转。将父节点的颜色设置为”黑色“后,将祖父节点设置为”红色“并为祖父节点应用右旋转。
4) 为根设置黑色。
*/
balanceInsert(node) {
// 当父节点是”红色“时需要平衡
while (node.parent.color === CONSTANTS.RED) {
// 父节点是祖父节点的左侧子节点
if (node.parent === node.parent.parent.left) {
const uncle = node.parent.parent.right;
// 如果叔节点和父节点都是”红色“,需要把这些”黑色“和祖父节点变成”红色“
if (uncle.color === CONSTANTS.RED) {
uncle.color = CONSTANTS.BLACK;
node.parent.color = CONSTANTS.BLACK;
node.parent.parent.color = CONSTANTS.RED;
node = node.parent.parent;
}
// 如果父节点是”红色“,叔节点是”黑色“
else {
// 如果节点是右侧子节点
if (node === node.parent.right) {
node = node.parent;
this.rotateLeft(node);
}
node.parent.color = CONSTANTS.BLACK;
node.parent.parent.color = CONSTANTS.RED;
this.rotateRight(node.parent.parent);
}
} else {
const uncle = node.parent.parent.left;
if (uncle.color === CONSTANTS.RED) {
uncle.color = CONSTANTS.BLACK;
node.parent.color = CONSTANTS.BLACK;
node.parent.parent.color = CONSTANTS.RED;
node = node.parent.parent;
} else {
if (node == node.parent.left) {
node = node.parent;
this.rotateRight(node);
}
node.parent.color = CONSTANTS.BLACK;
node.parent.parent.color = CONSTANTS.RED;
this.rotateLeft(node.parent.parent);
}
}
if (node == this.root) {
break;
}
}
this.root.color = CONSTANTS.BLACK;
}
//左旋转
//-----------------------------
rotateLeft(node) {
const vertex = node.right;
// 为顶点设置新的右侧节点
node.right = vertex.left;
if (vertex.left != this.leaf) {
vertex.left.parent = node;
}
// 用新节点替换节点
vertex.parent = node.parent;
// 如果节点是根,则设置新根节点
if (! node.parent) {
this.root = vertex;
}
// 替换父节点
else if (node === node.parent.left) {
node.parent.left = vertex;
}
else {
node.parent.right = vertex;
}
// 为顶点设置左侧子节点
vertex.left = node;
node.parent = vertex;
}
//右旋转
//-----------------------------
rotateRight(node) {
// 左侧子节点是新顶点
const vertex = node.left;
// 节点丢失左子节点,我们用新顶点的右侧子节点替换它
node.left = vertex.right;
if (vertex.right != this.leaf) {
vertex.right.parent = node;
}
// 新顶点替换旧节点
vertex.parent = node.parent;
if (! node.parent) {
this.root = vertex;
} else if (node == node.parent.right) {
node.parent.right = vertex;
} else {
node.parent.left = vertex;
}
// 为新顶点附加右子节点 - 它是旧节点
vertex.right = node;
node.parent = vertex;
}
//搜索最小值的节点
//-----------------------------
minimum(node) {
while (node.left != this.leaf) {
node = node.left;
}
return node;
}
//交换节点
//-----------------------------
swap(oldNode, newNode) {
if (! oldNode.parent) {
this.root = newNode;
} else if (oldNode == oldNode.parent.left) {
oldNode.parent.left = newNode;
} else {
oldNode.parent.right = newNode;
}
newNode.parent = oldNode.parent;
}
//删除节点
//-----------------------------
deleteNode(key) {
let forRemove = this.leaf;
let tmp = this.root;
// 搜索要删除的节点
while (tmp != this.leaf) {
if (tmp.key === key) {
forRemove = tmp;
break;
}
if (tmp.key > key) {
tmp = tmp.left;
} else {
tmp = tmp.right;
}
}
if (forRemove == this.leaf) {
console.log('node not found');
return;
}
let minRight = forRemove;
let minRightColor = minRight.color;
let newMinRight;
// 如果要移除的节点没有左侧子节点, 用它的右侧子节点替换它
if (forRemove.left == this.leaf) {
newMinRight = forRemove.right;
this.swap(forRemove, forRemove.right);
}
// 如果要移除的节点没有右侧子节点, 用它的左侧子节点替换它
else if (forRemove.right == this.leaf) {
newMinRight = forRemove.left;
this.swap(forRemove, forRemove.left);
}
// 如果要删除的节点有两个子节点
else {
minRight = this.minimum(forRemove.right);
minRightColor = minRight.color;
newMinRight = minRight.right;
if (minRight.parent === forRemove) {
newMinRight.parent = minRight;
}
// 用右子树替换右子树的最小值 (从节点附加右子节点以移除到右子树的最小值 )
else {
this.swap(minRight, minRight.right);
minRight.right = forRemove.right;
minRight.right.parent = minRight;
}
// 从节点附加左子节点以移除到右子树的最小值
this.swap(forRemove, minRight);
minRight.left = forRemove.left;
minRight.left.parent = minRight;
minRight.color = forRemove.color;
}
if (minRightColor === CONSTANTS.BLACK) {
this.balanceDelete(newMinRight);
}
}
//平衡删除的节点
//-----------------------------
/*
删除后平衡树的方法:
1)在节点不是树的根且节点的颜色为"黑色"时对树进行平衡
2)如果节点是其父节点的左子节点
a) 如果节点的兄弟节点是”红色“:设置兄弟的颜色为”黑色“,设置父节点的颜色为”红色“。将左旋转应用于节点的父节点。将父节点的右侧子节点设置为兄弟节点。
b) 如果兄弟节点的子节点是”黑色“:将兄弟节点的颜色设置为”红色“,并对节点的父节点应用平衡。
c) 如果兄弟节点的一个子节点的颜色是”红色“。如果兄弟节点的右侧子节点颜色为”黑色“:设置左侧子节点的颜色为”黑色“,设置兄弟节点的颜色为”红色“,对兄弟节点应用右旋转,设置父节点的右侧子节点为兄弟节点。之后,设置兄弟节点的颜色等于父节点的颜色,设置父节点颜色为”黑色“,设置兄弟节点的右侧子节点颜色为”黑色“。将左旋转应用于节点的父节点。将树的根设置为节点。
3)如果节点是右侧子节点,他的兄弟节点是左侧子节点。
a) 如果兄弟节点的颜色是”红色“。将兄弟节点的颜色设置为”黑色“,将父节点的颜色设置为”红色“,对节点的父节点应用右旋转,并将父节点的左侧子节点分配为兄弟。
b) 如果兄弟节点的两个子节点都是”黑色“。将兄弟节点的颜色设置为”红色“并将平衡应用于父节点。
c) 如果兄弟节点的一个子节点是”红色“的。如果兄弟节点的左侧子节点是”黑色“,则将兄弟节点的右侧子节点的颜色设置为”黑色“,将兄弟节点的颜色设置为”红色“,对兄弟节点应用左旋转,将父节点的左侧子节点设置为兄弟节点。之后,将兄弟节点的颜色设置为父节点的颜色。将父节点的颜色设置为”黑色“,将兄弟节点的左侧子节点的颜色设置为”黑色“,将右旋转应用于父节点。将根设置为节点。
*/
balanceDelete(node) {
while (node != this.root && node.color == CONSTANTS.BLACK) {
if (node == node.parent.left) {
let brother = node.parent.right;
if (brother.color == CONSTANTS.RED) {
brother.color = CONSTANTS.BLACK;
node.parent.color = CONSTANTS.RED;
this.rotateLeft(node.parent);
brother = node.parent.right;
}
if (
brother.left.color == CONSTANTS.BLACK &&
brother.right.color == CONSTANTS.BLACK
) {
brother.color = CONSTANTS.RED;
node = node.parent;
} else {
if (brother.right.color == CONSTANTS.BLACK) {
brother.left.color = CONSTANTS.BLACK;
brother.color = CONSTANTS.RED;
this.rotateRight(brother);
brother = node.parent.right;
}
brother.color = node.parent.color;
node.parent.color = CONSTANTS.BLACK;
brother.right.color = CONSTANTS.BLACK;
this.rotateLeft(node.parent);
node = this.root;
}
} else {
let brother = node.parent.left
if (brother.color == CONSTANTS.RED) {
brother.color = CONSTANTS.BLACK;
node.parent.color = CONSTANTS.RED;
this.rotateRight(node.parent);
brother = node.parent.left;
}
if (
brother.left.color == CONSTANTS.BLACK &&
brother.right.color == CONSTANTS.BLACK
) {
brother.color = CONSTANTS.RED;
node = node.parent;
} else {
if (brother.left.color == CONSTANTS.BLACK) {
brother.right.color = CONSTANTS.BLACK;
brother.color = CONSTANTS.RED;
this.rotateLeft(brother);
brother = node.parent.left;
}
brother.color = node.parent.color;
node.parent.color = CONSTANTS.BLACK;
brother.left.color = CONSTANTS.BLACK;
this.rotateRight(node.parent);
node = this.root;
}
}
}
node.color = CONSTANTS.BLACK;
}
//打印节点结构
//-----------------------------
printTree() {
const stack = [
{ node: this.root, str: '' },
];
while (stack.length) {
// 删除最后一个元素
const item = stack.pop();
// Don't print empty leaf
if (item.node == this.leaf) {
continue;
}
// 获得左或者右节点的位置
let position = '';
if (item.node.parent) {
position = item.node === item.node.parent.left ? 'L----' : 'R----';
} else {
position = 'ROOT-';
}
console.log(`${item.str}${position} ${item.node.key} (${item.node.color})`);
// 将节点的子节点添加到堆栈中
stack.push({ node: item.node.right, str: item.str + ' ' });
stack.push({ node: item.node.left, str: item.str + ' | ' });
}
}
}
const t = new RedBlackTree();
for (let i = 1; i < 20; i++) {
t.insert({ key: i });
}
t.printTree();
/*
ROOT- 8 (BLACK)
| L---- 4 (RED)
| | L---- 2 (BLACK)
| | | L---- 1 (BLACK)
| | R---- 3 (BLACK)
| R---- 6 (BLACK)
| | L---- 5 (BLACK)
| R---- 7 (BLACK)
R---- 12 (RED)
| L---- 10 (BLACK)
| | L---- 9 (BLACK)
| R---- 11 (BLACK)
R---- 14 (BLACK)
| L---- 13 (BLACK)
R---- 16 (RED)
| L---- 15 (BLACK)
R---- 18 (BLACK)
| L---- 17 (RED)
R---- 19 (RED)
*/
for (let i = 1; i < 20; i++) {
if (i % 3 === 0) {
t.deleteNode(i);
}
}
t.printTree();
/*
ROOT- 8 (BLACK)
| L---- 4 (BLACK)
| | L---- 2 (BLACK)
| | | L---- 1 (RED)
| R---- 7 (BLACK)
| | L---- 5 (RED)
R---- 14 (RED)
| L---- 11 (BLACK)
| | L---- 10 (BLACK)
| R---- 13 (BLACK)
R---- 17 (BLACK)
| L---- 16 (BLACK)
R---- 19 (BLACK)
*/
堆(特殊的二叉树,二叉堆)
二叉树有两种表示形式:指针(参看上面的案例)和数组(使用索引)
/*
比如数字通常存储为 1 2 3 4 5 6 7
变成堆的数据结构则为(注意索引顺序是0,1,2,3,4,5,6排列):
注意:堆的索引都是不变的,按顺序从二叉树由上至下。
下面的二叉树使用索引来检索位置
1(0)
/ \
2(1) 3(2)
/ \ / \
4(3) 5(4) 6(5) 7(6)
*/
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1
};
function defaultCompare(a, b) {
if (a === b) {
return 0;
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
function reverseCompare(compareFn) {
return (a, b) => compareFn(b, a);
}
function swap(array, a, b) {
/* const temp = array[a];
array[a] = array[b];
array[b] = temp; */
[array[a], array[b]] = [array[b], array[a]];
}
/* 也可使用ES6简写(数组解构性能比上面的原生方式差)
const swap = (arr,a,b) => [arr[a], arr[b]] = [arr[b], arr[a]];
*/
//创建最小堆类
class MinHeap {
constructor(compareFn = defaultCompare) {
this.compareFn = compareFn;
this.heap = [];
}
//左侧子节点的位置 2*index+1(如果位置可用,参看之前示例的索引排列方式)
getLeftIndex(index) {
return (2 * index) + 1;
}
//右侧子节点的位置 2*index+2(如果位置可用,参看之前示例的索引排列方式)
getRightIndex(index) {
return (2 * index) + 2;
}
//父节点的位置是 index/2(如果位置可用,参看之前示例的索引排列方式)
getParentIndex(index) {
if (index === 0) {
return undefined;
}
return Math.floor((index - 1) / 2); //只保留整数,向下取整(下舍)
}
size() {
return this.heap.length;
}
isEmpty() {
return this.size() <= 0;
}
clear() {
this.heap = [];
}
findMinimum() {
return this.isEmpty() ? undefined : this.heap[0];
}
insert(value) {
if (value != null) {
const index = this.heap.length;
this.heap.push(value);
this.siftUp(index);
return true;
}
return false;
}
//下移操作(堆化)
siftDown(index) {
let element = index;
const left = this.getLeftIndex(index);
const right = this.getRightIndex(index);
const size = this.size();
if (
left < size
&& this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN
) {
element = left; //元素比左侧节点大
}
if (
right < size
&& this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
) {
element = right; //元素比右侧节点大
}
if (index !== element) {
swap(this.heap, index, element);
this.siftDown(element);
}
}
//上移操作
siftUp(index) {
let parent = this.getParentIndex(index);
while (
index > 0
&& this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
) {
swap(this.heap, parent, index);
index = parent;
parent = this.getParentIndex(index); //基线条件
}
}
//导出最大值最小值(删除它们)
extract() {
if (this.isEmpty()) {
return undefined;
}
if (this.size() === 1) {
return this.heap.shift(); // 删除第一个元素并返回
}
const removedValue = this.heap[0];
this.heap[0] = this.heap.pop(); //用最后一个元素补上
this.siftDown(0); //下移操作
return removedValue;
}
//用于堆排序算法
heapify(array) {
if (array) {
this.heap = array;
}
const maxIndex = Math.floor(this.size() / 2) - 1;
for (let i = 0; i <= maxIndex; i++) {
this.siftDown(i);
}
return this.heap;
}
getAsArray() {
return this.heap;
}
}
//创建最大堆类(把所有大于比较换成小于,最大值是堆的根节点)
class MaxHeap extends MinHeap {
constructor(compareFn = defaultCompare) {
super(compareFn);
this.compareFn = compareFn;
this.compareFn = reverseCompare(compareFn);
}
}
//使用:
const heap = new MinHeap();
heap.insert(2);
heap.insert(3);
heap.insert(4);
heap.insert(5);
heap.insert(1);
console.log(heap.heap); // [1, 2, 4, 5, 3]
/*
最小堆:最小值总是位于数组第一个位置(根节点)
括号内是索引:
1(0)
/ \
2(1) 4(2)
/ \
5(3) 3(4)
*/
堆排序算法:
function heapify(array, index, heapSize, compareFn) {
let largest = index;
const left = (2 * index) + 1;
const right = (2 * index) + 2;
if (left < heapSize && compareFn(array[left], array[index]) > 0) {
largest = left;
}
if (right < heapSize && compareFn(array[right], array[largest]) > 0) {
largest = right;
}
if (largest !== index) {
swap(array, index, largest);
heapify(array, largest, heapSize, compareFn);
}
}
function buildMaxHeap(array, compareFn) {
for (let i = Math.floor(array.length / 2); i >= 0; i -= 1) {
heapify(array, i, array.length, compareFn);
}
return array;
}
//堆排序算法
function heapSort(array, compareFn = defaultCompare) {
let heapSize = array.length;
buildMaxHeap(array, compareFn); //步骤1:用数组创建一个最大堆用作源数据
while (heapSize > 1) {
swap(array, 0, --heapSize); //步骤2:创建最大堆后,最大值会被存储在堆的第一个位置。要将它替换为堆的最后一个值,将堆的大小减1
heapify(array, 0, heapSize, compareFn); //步骤3:将堆的根节点下移并重复步骤2,直到堆的大小为1
}
return array;
}
/*
注意:堆的索引都是不变的,按顺序从二叉树由上至下。
7
/ \
6 3
/ \ / \
5 4 1 2
排序后:
1
/ \
2 3
/ \ / \
4 5 6 7
*/
图
与树的区别: 树定义为层次结构,且只有一个双亲
遍历方式:
- 1.广度优先(breadth-first searh, BFS)
使用队列,将顶点存入队列,最先入队的顶点先被探索
- 2.深度优先(depth-first search,DFS)
使用栈,从第一个指定的顶点开始,存在新的相邻顶点就去访问,顺序类似二叉树的前序遍历
/*
注意图的顶点,路径,度(一个顶点相邻的边的数量),环,邻接矩阵
A
/ \
B C
/ \
D E
使用邻接表的动态数据结构来表示图:
A | B C
B | D E
C |
D |
E |
使用邻接矩阵 (有向):
| A B C D E
──|──────────
A | 0 1 1 0 0
B | 0 0 0 1 1
C | 0 0 0 0 0
D | 0 0 0 0 0
E | 0 0 0 0 0
邻接矩阵可以声明为:
const graph = [
[0,1,1,0,0],
[0,0,0,1,1],
[0,0,0,0,0],
[0,0,0,0,0],
[0,0,0,0,0]
]
//然后遍历寻找最短路径
*/
//使用字典类来创建
class Graph {
constructor(isDirected = false) { //默认情况图是无向的
this.isDirected = isDirected;
this.vertices = [];
this.adjList = new Map();
}
addVertex(v) {
if (!this.vertices.includes(v)) {
this.vertices.push(v);
this.adjList.set(v, []); // initialize adjacency list with array as well;
}
}
addEdge(a, b) {
if (!this.adjList.get(a)) {
this.addVertex(a);
}
if (!this.adjList.get(b)) {
this.addVertex(b);
}
this.adjList.get(a).push(b);
if (this.isDirected !== true) {
this.adjList.get(b).push(a);
}
}
getVertices() {
return this.vertices;
}
getAdjList() {
return this.adjList;
}
toString() {
let s = '';
for (let i = 0; i < this.vertices.length; i++) {
s += `${this.vertices[i]} -> `;
const neighbors = this.adjList.get(this.vertices[i]);
for (let j = 0; j < neighbors.length; j++) {
s += `${neighbors[j]} `;
}
s += '\n';
}
return s;
}
}
//用法:
const graph = new Graph(true);
const myVertices = ['A','B','C','D','E'];
for (let i =0; i< myVertices.length; i++) {
graph.addVertex(myVertices[i]);
}
graph.addEdge('A','B');
graph.addEdge('A','C');
graph.addEdge('B','D');
graph.addEdge('B','E');
console.log( graph.toString() );
/*
有向的(将Graph参数设置为true)
A -> B C
B -> D E
C ->
D ->
E ->
无向的:
A -> B C
B -> A D E
C -> A
D -> B
E -> B
*/
// 广度优先搜索
//--------------
//枚举器
//0表示顶点未被访问, 1表示顶点被访问过但没有被探索,2表示已被探索
const Colors = {
WHITE: 0,
GREY: 1,
BLACK: 2
};
const initializeColor = vertices => {
const color = {};
for (let i = 0; i < vertices.length; i++) {
color[vertices[i]] = Colors.WHITE;
}
return color;
};
const breadthFirstSearch = (graph, startVertex, callback) => {
const vertices = graph.getVertices();
const adjList = graph.getAdjList();
const color = initializeColor(vertices);
const queue = new Queue();
queue.enqueue(startVertex);
while (!queue.isEmpty()) {
const u = queue.dequeue(); // 队列头部(移除一个顶点,并取得包含其所有邻点的邻接表)
const neighbors = adjList.get(u);
color[u] = Colors.GREY;
for (let i = 0; i < neighbors.length; i++) {
const w = neighbors[i];
if (color[w] === Colors.WHITE) {
color[w] = Colors.GREY;
queue.enqueue(w);
}
}
color[u] = Colors.BLACK;
if (callback) {
callback(u);
}
}
};
breadthFirstSearch(graph, myVertices[0], function(v) {
console.log(v);
});
/*搜索顺序输出:
A
B
C
D
E
*/
//找到最小距离
//---------
const BFS = (graph, startVertex) => {
const vertices = graph.getVertices();
const adjList = graph.getAdjList();
const color = initializeColor(vertices);
const queue = new Queue();
const distances = {}; //距离
const predecessors = {}; //前溯点(相当于父节点)
queue.enqueue(startVertex);
for (let i = 0; i < vertices.length; i++) {
distances[vertices[i]] = 0;
predecessors[vertices[i]] = null;
}
while (!queue.isEmpty()) {
const u = queue.dequeue();
const neighbors = adjList.get(u);
color[u] = Colors.GREY;
for (let i = 0; i < neighbors.length; i++) {
const w = neighbors[i];
if (color[w] === Colors.WHITE) {
color[w] = Colors.GREY;
distances[w] = distances[u] + 1;
predecessors[w] = u;
queue.enqueue(w);
}
}
color[u] = Colors.BLACK;
}
return {
distances,
predecessors
};
};
//使用
const shortestPathA = BFS(graph, myVertices[0]);
console.log(shortestPathA);
/*
{
"distances": {
"A": 0,
"B": 1,
"C": 1,
"D": 2,
"E": 2
},
"predecessors": {
"A": null,
"B": "A",
"C": "A",
"D": "B",
"E": "B"
}
}
A到B,C的距离为1,到D,E的距离为2 (边的数量)
*/
//利用前溯点可输出顶点A的所有完整路径:
const fromVertex = myVertices[0];
for (i = 1; i < myVertices.length; i++) {
const toVertex = myVertices[i];
const path = [];
for (let v = toVertex; v !== fromVertex; v = shortestPathA.predecessors[v]) {
path.push(v);
}
path.push(fromVertex);
let s = path.pop(); //最后一个加入栈的,也是第一个被弹出的项
while ( path.length > 0 ) {
s += ' - ' + path.pop();
}
console.log( s );
}
/*
输出:
A - B
A - C
A - B - D
A - B - E
*/
// 深度优先搜索(需要使用递归,来实现类似二叉搜索树的前序遍历的顺序)
//--------------
//枚举器
//0表示顶点未被访问, 1表示顶点被访问过但没有被探索,2表示已被探索
const Colors = {
WHITE: 0,
GREY: 1,
BLACK: 2
};
const initializeColor = vertices => {
const color = {};
for (let i = 0; i < vertices.length; i++) {
color[vertices[i]] = Colors.WHITE;
}
return color;
};
const depthFirstSearch = (graph, callback) => {
const vertices = graph.getVertices();
const adjList = graph.getAdjList();
const color = initializeColor(vertices);
for (let i = 0; i < vertices.length; i++) {
if (color[vertices[i]] === Colors.WHITE) {
depthFirstSearchVisit(vertices[i], color, adjList, callback);
}
}
};
const depthFirstSearchVisit = (u, color, adjList, callback) => {
color[u] = Colors.GREY;
if (callback) {
callback(u);
}
// console.log('Discovered ' + u);
const neighbors = adjList.get(u);
for (let i = 0; i < neighbors.length; i++) {
const w = neighbors[i];
if (color[w] === Colors.WHITE) {
depthFirstSearchVisit(w, color, adjList, callback);
}
}
color[u] = Colors.BLACK;
// console.log('explored ' + u);
};
depthFirstSearch(graph, function(v) {
console.log(v);
});
/*搜索顺序输出:
A
B
D
E
C
*/
//找到最小距离
//---------
const DFSVisit = (u, color, d, f, p, time, adjList) => {
// console.log('discovered ' + u);
color[u] = Colors.GREY;
d[u] = ++time.count;
const neighbors = adjList.get(u);
for (let i = 0; i < neighbors.length; i++) {
const w = neighbors[i];
if (color[w] === Colors.WHITE) {
p[w] = u;
DFSVisit(w, color, d, f, p, time, adjList);
}
}
color[u] = Colors.BLACK;
f[u] = ++time.count;
// console.log('explored ' + u);
};
const DFS = graph => {
const vertices = graph.getVertices();
const adjList = graph.getAdjList();
const color = initializeColor(vertices);
const d = {};
const f = {};
const p = {};
const time = { count: 0 };
for (let i = 0; i < vertices.length; i++) {
f[vertices[i]] = 0;
d[vertices[i]] = 0;
p[vertices[i]] = null;
}
for (let i = 0; i < vertices.length; i++) {
if (color[vertices[i]] === Colors.WHITE) {
DFSVisit(vertices[i], color, d, f, p, time, adjList);
}
}
return {
discovery: d,
finished: f,
predecessors: p
};
};
//使用
const depthPrint = DFS(graph);
console.log(depthPrint);
/*
{
"discovery": {
"A": 1,
"B": 2,
"C": 8,
"D": 3,
"E": 5
},
"finished": {
"A": 10,
"B": 7,
"C": 9,
"D": 4,
"E": 6
},
"predecessors": {
"A": null,
"B": "A",
"C": "A",
"D": "B",
"E": "B"
}
}
*/
本文出自没位道 - Chuckie Chang个人网站,转载请保留出处,谢谢!
文章采用 知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。







文章评论